Tic-Tac-Toe was too easy …
You can win this time.
Ultimate Tic-tac-toe
Ultimate tic-tac-toe is a board game composed of nine tic-tac-toe boards arranged in a 3 × 3 grid. Players take turns playing in the smaller tic-tac-toe boards until one of them wins in the larger tic-tac-toe board.
The game starts with X playing wherever they want in any of the 81 empty spots. This move “sends” their opponent to its relative location. For example, if X played in the top right square of their local board, then O needs to play next in the local board at the top right of the global board. O can then play in any one of the nine available spots in that local board, each move sending X to a different local board.
If a move is played so that it is to win a local board by the rules of normal tic-tac-toe, then the entire local board is marked as a victory for the player in the global board.
Once a local board is won by a player or it is filled completely, no more moves may be played in that board. If a player is sent to such a board, then that player may play in any other board.
Monte Carlo Tree Search
Monte Carlo Tree Search (MCTS) is a search technique in the field of Artificial Intelligence (AI).
The focus of MCTS is on the analysis of the most promising moves, expanding the search tree based on random sampling of the search space. The application of Monte Carlo tree search in games is based on many playouts. In each playout, the game is played out to the very end by selecting moves at random. The final game result of each playout is then used to weight the nodes in the game tree so that better nodes are more likely to be chosen in future playouts.
Each round of Monte Carlo tree search consists of four steps:
- Selection: Start from root R and select successive child nodes until a leaf node L is reached. The root is the current game state and a leaf is any node that has a potential child from which no simulation (playout) has yet been initiated.
- Expansion: Unless L ends the game decisively (e.g. win/loss/draw) for either player, create one (or more) child nodes and choose node C from one of them. Child nodes are any valid moves from the game position defined by L.
- Simulation: Complete one random playout from node C. A playout may be as simple as choosing uniform random moves until the game is decided (for example in chess, the game is won, lost, or drawn).
- Backpropagation: Use the result of the playout to update information in the nodes on the path from C to R.
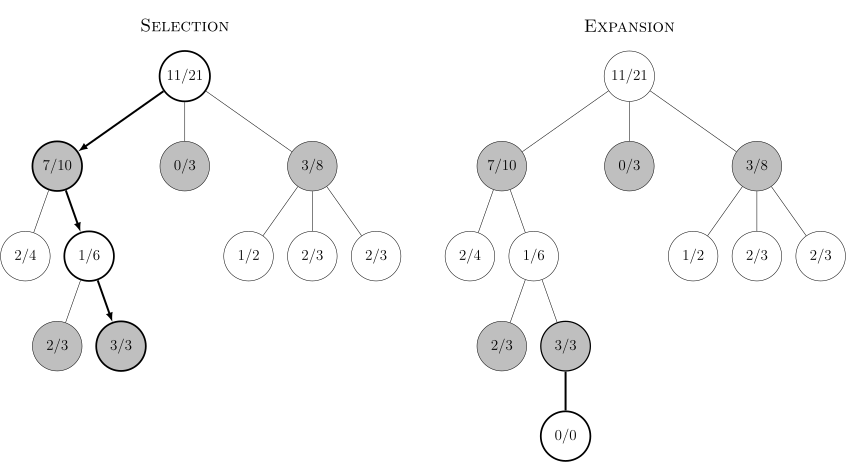

This graph shows the steps involved in one decision, with each node showing the ratio of wins to total playouts from that point in the game tree for the player that the node represents. In the Selection diagram, black is about to move. The root node shows there are 11 wins out of 21 playouts for white from this position so far. It complements the total of 10/21 black wins shown along the three black nodes under it, each of which represents a possible black move.
If white loses the simulation, all nodes along the selection incremented their simulation count (the denominator), but among them only the black nodes were credited with wins (the numerator). If instead white wins, all nodes along the selection would still increment their simulation count, but among them only the white nodes would be credited with wins. In games where draws are possible, a draw causes the numerator for both black and white to be incremented by 0.5 and the denominator by 1. This ensures that during selection, each player’s choices expand towards the most promising moves for that player, which mirrors the goal of each player to maximize the value of their move.
Rounds of search are repeated as long as the time allotted to a move remains. Then the move with the most simulations made (i.e. the highest denominator) is chosen as the final answer.
Exploitation vs Exploation
The main difficulty in selecting child nodes is maintaining some balance between the exploitation of deep variants after moves with high average win rate and the exploration of moves with few simulations. The first formula for balancing exploitation and exploration in games is UCT (Upper Confidence Bound 1 applied to trees). It is recommended to choose in each node of the game tree the move for which the following expression has the highest value :

- wi stands for the number of wins for the node considered after the i-th move
- ni stands for the number of simulations for the node considered after the i-th move
- Ni stands for the total number of simulations after the i-th move run by the parent node of the one considered
- c is the exploration parameter—theoretically equal to √2; in practice usually chosen empirically
The first component of the formula above corresponds to exploitation; it is high for moves with high average win ratio. The second component corresponds to exploration; it is high for moves with few simulations.